IntGen¶
To give a full example, let’s take numerical integration. If a code uses an
integral with discrete and symbolic parts, there are huge gains if the code
evaluates the symbolic parts before they are run. For example take the
following integral, where 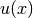 comes from a discrete function in the code:
comes from a discrete function in the code:
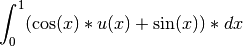
A quick optimization would be to evaluate 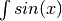 and
and 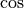 at the quadrature points, assuming two quadrature points, the new code would
be:
at the quadrature points, assuming two quadrature points, the new code would
be:
![0.45969769 + 0.48887694*u[0] + 0.35239291*u[1]](../images/math/0c05b6c49fb6526e15df30276ff953e08ff34e77.png)
But that code is meaningless with out the formula above! What’s more the user has to evaluate the symbolic parts by hand which becomes yet another source of error. It would be better to have a high level code that generates the low level code when a new integral (or even better precision) is required.
Using IntGen¶
In IntGen the above integral is translated into the following code:
u = DiscFunc("u")
x = Symbol("x")
dx = Dom(x, 0, 1)
integral = (Func(cos(x), x)*u + Func(sin(x), x))*dx
select_quad_rule(num_pts=2, name="Gauss")
gen_file("ex1", [integral], ["eval_gen"], ['u'])
And the generated file that implements the integral would be:
const unsigned int NUM_QUAD_PTS = 2;
const double QUAD_PTS[2] = {-0.57735026919, 0.57735026919};
const double QUAD_WTS[2] = {1.0, 1.0};
inline double eval_gen(double* u)
{
double ret_val = 0.0;
ret_val += 0.459697694131860;
ret_val += 0.488876937571022*(u[0])
+ 0.352392910067197*(u[1]);
return ret_val;
}
For the full example see demo/int_gen.